Guilherme Henrique da Silva Pinto Geotechnical Engineer, Pimenta de Ávila Consultoria, Nova Lima, Brazil,
André de Oliveira Faria Geotechnical Engineer, Pimenta de Ávila Consultoria, Nova Lima, Brazil,
Mauro Pio dos Santos Junior Geotechnical Coordinator, Pimenta de Ávila Consultoria, Nova Lima, Brazil.
Abstract
Determining the undrained shear strength of contractive materials is of fundamental importance to evaluate the stability condition of geotechnical structures. Commonly, this evaluation is performed using laboratory tests, such as the isotropically consolidated undrained triaxial compression test (CIUC), or field tests, such as the Field Vane Shear Test (FVST) and the Cone Penetration Test (CPTu). Based on the CPTu, different methodologies (empirical and/or analytical) were developed in the literature to assess the undrained shear strength. This paper aims to evaluate the yield and remolded undrained shear strength of a bauxite tailings, using field and laboratory tests. The yield undrained shear strength was calculated based on the CPTu test using the classical equations based on bearing capacity factors (Nkt, Nke and NΔu), considering three methodologies: i) Mantaras et al. (2014); ii) Mayne & Peuchen (2018) and iii) Mayne et al. (2023). The remolded undrained shear strength was determined based on the sleeve friction of the CPTu, following the classical equation developed by Robertson et al. (1986). The values obtained were compared with the CIUC tests (with and without correction to account for anisotropic consolidation) and the FVST. The results have shown that: i) if accounted for anisotropic consolidation, the laboratory results are similar to the values determined using Nkt and NΔu ii) possibly due to the inaccuracy of the measurement of the sleeve friction (fs), the remolded undrained shear strength measured using the CPTu showed lower results than the FVST.
Introduction
The correct measurement of tailings properties such as its strength and stiffness are highly important in geotechnical engineering since they are used to evaluate the stability condition of a Tailings Storage Facility (TSF). If the geotechnical parameters are not adequately determined, the TSF may either be over- dimensioned or, in the worst situation, it may not present the necessary resilience to the expected loads it will face throughout its life cycle.
To evaluate the tailings characteristics and its behavior, geotechnical engineers usually perform laboratory and field tests to assess proprieties such as grain-size distribution, Atterberg limits, stiffness, drainage conditions and shear strength. Among the commercially available field tests, the Field Vane Shear Test (FVST) and the Cone Penetration Test (CPTu) are the most often used.
The undrained shear strength (Su) can be defined as the geomaterial shear resistance in a saturated or nearly saturated condition, mobilized under a fast loading without allowing time for volumetric change (Lunne et al., 1997). In contractile materials, the generated porewater pressure is positive, which reduces the effective stress and, therefore, its shear strength. The undrained shear strength can be calculated by the CPTu using equations based on the bearing capacity factors (Nkt, NΔu and Nke) as described by Lunne et al. (1997), or directly measured by the FVST and the laboratory tests (such as triaxial compression, and direct simple shear).
To determine the bearing capacity factors, several methodologies (analytical and/or empirical) have been published in the literature based on CPTu data, such as Mantaras et al. (2014), Mayne & Peuchen (2018), Mayne et al. (2023), and others. Most of these methodologies were developed for natural soils. The reliability of these proposes must be evaluated when applied in tailings, since they present certain unique characteristics, such as geochemistry, angular particles, and potentially high compressibility.
This paper aims to present the evaluation of the undrained shear strength profile of a bauxite tailings using laboratory and field tests (CPTu and FVST). To perform the Nkt, NΔu and Nke calibration three methodologies were applied: i) Mantaras et al. (2014); ii) Mayne & Peuchen (2018) and iii) Mayne et al. (2023). The remolded undrained shear strength was determined based on the sleeve friction of the CPTu as suggested by Robertson et al. (1986). Additionally, the results obtained were compared with the FVST (yield and remolded conditions) and the triaxial compression test (CIUC), with and without the correction to account for anisotropic consolidation.
Grain-Size Distribution and Atterberg Limits
The bauxite tailings evaluated in this study is the by-product of washing a bauxite ore at a mine in the state of Pará/Brazil. No chemicals were used in the ore processing. As indicated in Figure 1, the average particle- size distribution, using the American standard D422-63 criteria (ASTM, 2007) is: 2% sand; 28% silt; and 70% of clay size particles, with the mean value of the specific gravity (Gs) equal to 2.9. On average, the Atterberg Limits, determined according to the standard D4318-17 (ASTM, 2018), indicated a Liquid Limit (LL) of 55%, a Plastic Limit (LP) of 29% and Plasticity Index (PI) of 26%, classifying as a high plasticity clayey soil, just above the A-Line. These results were obtained as mean of 70 samples.
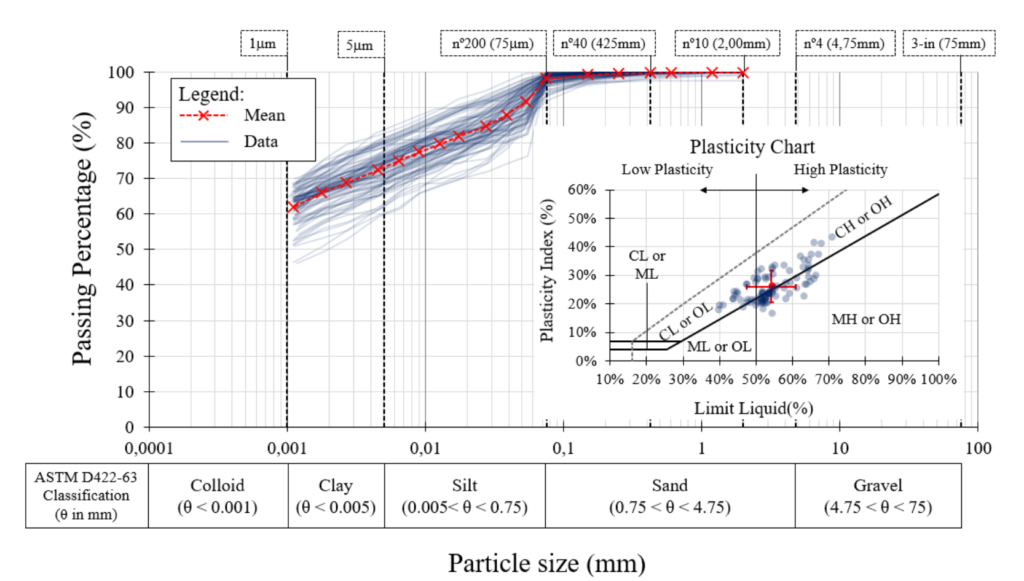
Figure 1: Particle size distribution and Plasticity Chart – Bauxite Tailings
In-situ Behavior
To evaluate the tailings in-situ behavior a Cone Penetration Test with Pore pressure measurement (CPTu) and 5 dissipation tests (DDP) was performed. The CPTu was performed as described by the international standard 22476-1 (ISO, 2022). The cone used has a cross-sectional area of 10 cm2, and the penetration was carried out at a rate of 2.0 ± 0.5 cm/s with readings taken every 5 cm. The CPTu performed with DDP provides four independent parameters: (i) the cone tip resistance (qc), which characterizes the soil resistance to cone penetration; (ii) the sleeve friction (fs), which represents the soil adhesion to the friction sleeve; (iii) the porewater pressure (u), commonly measured behind the cone tip (u2 location); and iv) the equilibrium in-situ porewater pressure (u0) obtained by the full stop of the cone penetration and the dissipation of the excess porewater pressure.
As described by Lunne et al. (1997), the total cone resistance qt can be calculated as qt = qc + u2 (1-a), where “a” is the cone area ratio, to account for the unequal end area effect. In this paper, the parameter “a” is equal to 0.82 as provided by the cone calibration certificate.
To evaluate the in-situ tailings behavior, the soil behavior type index proposed by Jefferies & Davies (1991) was applied using the normalized parameters presented by Equations 1 to 3, which are: Normalized Friction Ratio (FR), the Normalized Cone Resistance (Qt or Q) and pore pressure ratio (Bq), respectively. The classification system proposed by the authors should be understood as a behavior-based classification, since it does not measure physical characteristics, such as grain size or plasticity.
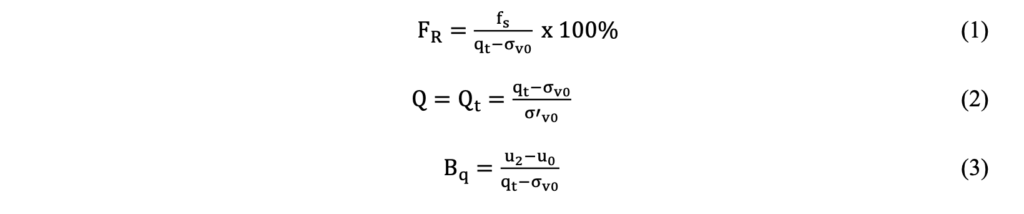
To evaluate the dilatancy, the analytical equation proposed by Dos Santos Junior (2021) to represent the contractive/dilative boundary suggested by Shuttle & Cunning (2008) was applied, as shown in Equation 4. Values plotted above the boundary are classified as dilative and values plotted below the boundary are classified as contractive.
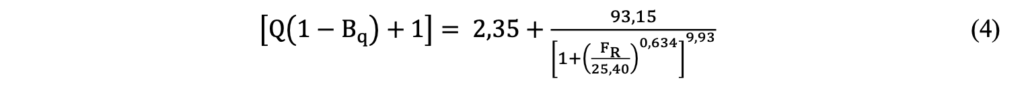
As a screening tool, the Bq was used to evaluate the tailings drainage condition. It was assumed that Bq values higher than 0.40 (Bq ≥ 0.40) represented an undrained response to the cone penetration. This criteria agrees with the range of values suggested by Schnaid (2009). An additional criterial was used in this paper to further evaluate the drainage condition during penetration. The Iq-Bq index (Equation 5, valid only to Bq > 0) proposed by Mayne et al. (2023). Using this criteria, the undrained penetration is assumed for values below 4.
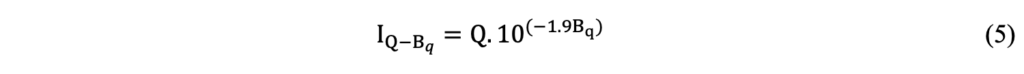
Figure 2 shows the CPTu primary data (qt, fs, u2 and Bq) for the test performed in the bauxite tailings, as well as the results of the dissipation tests. In the same figure is presented the equilibrium porewater pressure profile obtained by the interpolation of the dissipation tests (u0) and a 100% hydrostatic profile. Using the data from the CPTu, it was possible to distinguish three different materials: i) the unsaturated tailings, with the mean value of qt = 1 MPa and Bq < 0.40; ii) the saturated tailings, with the qt value around 0.50 MPa, showing a linear increase of qt and u2 over depth (normally consolidated behavior as detailed by Mayne et al., 2023), and values of Bq ≥ 0.40; and iii) the foundation soil with qt > 1.5 MPa and Bq approximately equal to 0.
Figure 2 also shows the five dissipation test curves obtained from the saturated tailings (the porepressure data and the normalized data). As can be seen, the bauxite tailings show a monotonic behavior with the porepressure reducing over time (dissipation of a positive excess of porewater pressure), characterizing a normally consolidated clay. Also, it is possible to note that the time for 50% consolidation (t50) is over 1000 seconds, which suggests an undrained condition according to Robertson (2010).
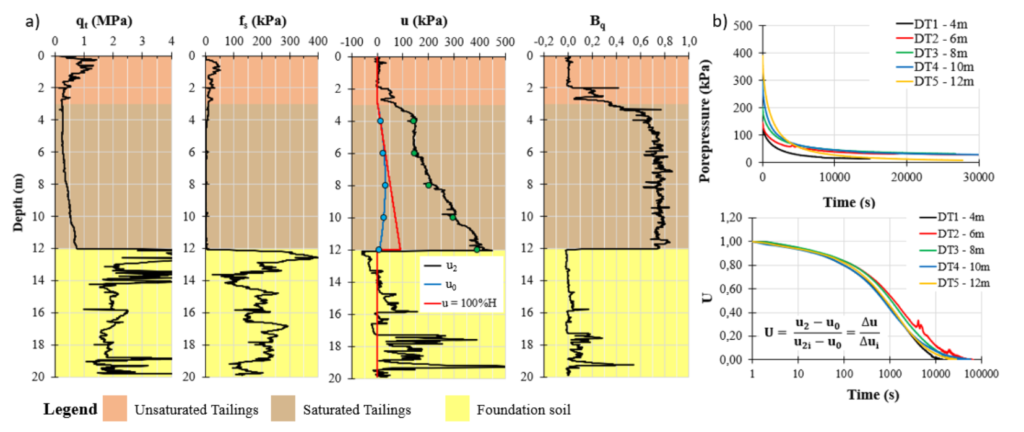Figure 2: Results of: a) the CPTu; and b) Dissipation tests.
Figure 3a shows the data of the CPTu performed in the bauxite tailings plotted in the soil-behavior type chart proposed by Jefferies & Davies (1991) using the boundary proposed by Dos Santos Junior (2021) to distinguish contractive and dilative behavior. Also, Figure 3b shows the contour of the IQ-Bq index prosed by Mayne et al. (2023) to evaluate the drainage condition of the penetration.
Figure 3: a) SBTn with Dos Santos Junior (2021) CD boundary; and b) IQ-Bq index proposed by Mayne et al. (2023)
As can be noted in Figure 3a, the saturated tailing (Bq ≥ 0.40) shows a contractive and clay-like behavior plotting below the boundary proposed by the author whereas the unsaturated tailing (Bq < 0.40) shows a dilative behavior ranging in terms of soil classification from clay to silty clay. This same behavior can be seen in Figure 3b, showing that the values of IQ-Bq index are lower than 4 for the saturated tailings and predominantly above 4 for the unsaturated tailings.
Undrained Shear Strength
To perform the calculation of the undrained shear strength using the CPTu data, three methodologies were used to determine the cone bearing factors Nkt, Nke and NΔu: i) Mantaras et al. (2014); ii) Mayne & Peuchen (2018) and iii) Mayne et al. (2023). The remolded undrained shear strength was also evaluated based on the sleeve friction measurement as suggested by Robertson et al. (1986). The results were compared with the FVST measurements and with a series of undrained triaxial compression tests (CIUC) with and without correction to account for anisotropic consolidation.
To predict the Su of contractive saturated (or nearly saturated) clayey materials, Lunne et al. (1997) present three different equations based on the bearing capacity factors. Equation 6 is based on net cone resistance (qnet = qt – σv0), Equation 7 is based on the excess porewater pressure (Δu = u2 – u0), and Equation 8 is based on the effective cone resistance (qeff. = qt – u2).
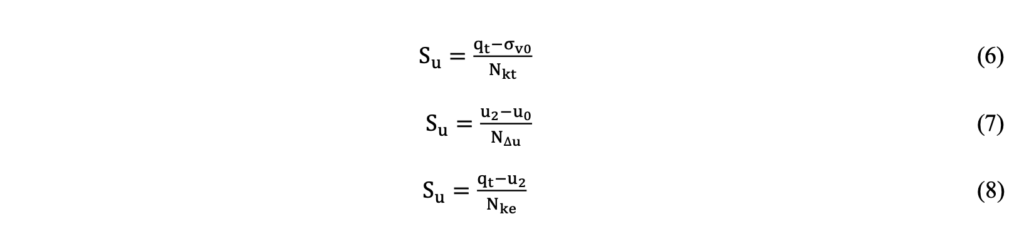
Mantaras et al. (2014)
Based on an analytical approach, Mantaras et al. (2014) prosed Equation 9 to calculate NΔu from the dissipation test, as a function of the Rigidity Index (IR) and the maximum excess of porewater pressure.
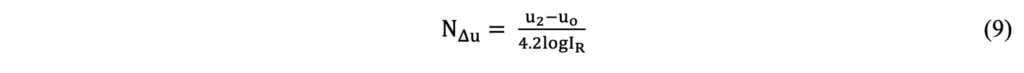
The Rigidity Index (IR) was calculated herein using the proposed equation by Agaiby & Mayne (2018) as indicated by Equation 10. The equation proposed by the authors is based on the hybrid formulation of Spherical Cavity Expansion and Critical State Soil Mechanics (SCE-CSSM). The slope of the critical state line (Mtc) was obtained from the triaxial compression tests and the parameter aq, proposed by the authors, is taken as the slope of the chart composed by u2 – σv0 (vertical axis) and qt – σv0 (horizontal axis).
Mayne & Peuchen (2018)
CHAPTER NAME
IR = exp [1.5+2.925 M aq] (10) M (1−aq)
Based on a database of high-quality triaxial compression tests with anisotropic consolidation (CAUC), for 62 different clays categorized into five groups based on their stress–history (ranging from fissured to sensitive clays), as well as for different test conditions (onshore and offshore), Mayne & Peuchen (2018) developed a relationship between Bq and the Nkt as expressed by the Equation 11.
Nkt = 10.5 − 4.6 ln(Bq + 0.1) (11)
Mayne et al. (2023)
Based on the same database of Mayne & Peuchen (2018), Mayne et al. (2023) proposed two different independent equations to evaluate the bearing capacity factors NΔu and Nke as indicated by Equations 12 and 13, respectively.
NΔu = 7.9 + 6.5 ln(Bq + 0.3) (12)
Nke = 4.5 − 10.66 ln(Bq + 0.2) (13)
Remolded undrained shear strength
As described by Robertson et al. (1986), the remolded shear strength of clays is approximately equal to the CPTu sleeve friction. Based on this, the estimation of this parameter can be performed by Equation 14.
fs = Su remolded (14)
Field Vane Shear Test (FVST)
The Field Vane Shear Test consists of a set of cruciform rectangular blades pushed to pre-defined depths with a rotation rate equal to 6.0±0.6o/min (ASTM D2573-08, 2008). The yield undrained shear strength is measured when the vane is pushed in the soil/tailings and the remolded condition after 10 complete rotations. Furthermore, the standard presents Equation 15 to evaluate the materials’ sensitivity, defined as the ratio of the yield undrained shear strength to the remolded undrained shear strength.
Triaxial Compression Test with Isotropic Consolidation (CIUC)
For this study, three undisturbed samples of the bauxite tailings were collected and nine CIUC tests were performed with the consolidation pressures of 50kPa, 100kPa, and 200kPa. Based on the test data, the following parameters were calculated: i) the normally consolidated undrained shear strength ratio (Su/σ’c = σd/2σ’c), as described by Olson & Mattson (2008), based on the maximum deviator stress (σd = σ1 – σ3) criteria; ii) the effective friction angle (φ′), assuming an effective cohesion equal to 0, as expected to a normally consolidated clay; and iii) the slope of the CSL in the q – p’ plane (M).
To correct the isotropic stress state from the CIUC (Su/σ’c) to the anisotropic in-situ condition (Su/σ’v0) and perform the correct comparison of the CIUC data with the field assessment, Equation 16 proposed by Jaky (1948) apud Mayne et al. (2023) and Equation 17 were used.
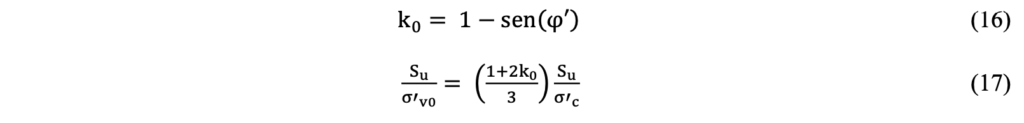
Undrained Shear Strength Profile
Figure 4 shows the results obtained from the CIUC tests. As can be seen, the samples generated a high shear–induced excess porewater pressure, even higher than the deviator stress. Also, it is noted that the bauxite tailings have a very ductile behavior, with no strength loss during shear, what is expected of high plastic tailings. The main results obtained were: i) Su/σ’c = 0.32; ii) φ’ = 27o with c’ = 0; and iii) Mtc = 1.72. Based on this data, the k0 value obtained was 0.55 and Su/σ’v0 equal to 0.22.
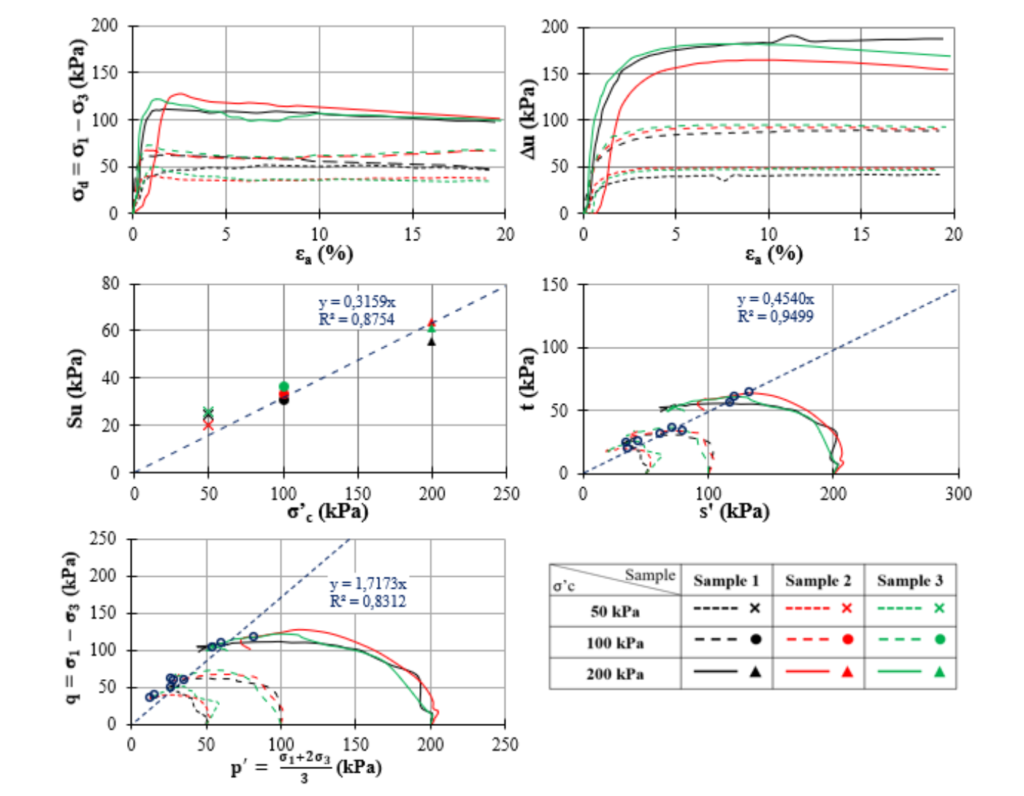
Figure 4: Isotropically consolidated undrained triaxial compression tests – Main Results
Equation 10 was used to calculate the IR for the bauxite tailings, in order to apply the methodology proposed by Mantaras et al. (2014). The aq parameter was obtained as shown in Figure 5, considering only the saturated portion of the tailings (undrained behavior). By using Mtc equal to 1.72 (Figure 4) and the aq value equal to 0.37 the IR value obtained was equal to 22.
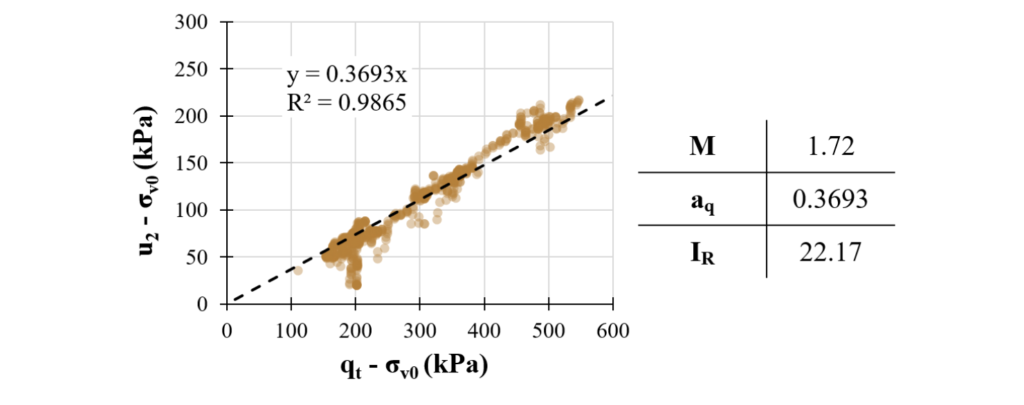
Figure 5: Calculation of the IR based on the aq parameter.
Figure 6 shows the comparison of the yield and remolded undrained shear strength considering all the field tests (CPTu and FVST) and laboratory tests (CIUC) available. In the evaluation presented herein it was only considered the tailings below 3,0 m of depth, since this is the region where undrained penetration of the cone was observed, as mentioned earlier in this paper. The surface of the tailings is subjected to weathering and high temperatures in the north of Brazil, creating an unsaturated crust (which is also observed in the field).
Figure 6, shows two different patterns of Su profile. The first one is obtained by the i) CIUC considering the undrained shear strength normalized by the consolidation pressure (Su/σ’c); ii) NΔu from Mantaras et al. (2014); and iii) Nke from Mayne et al. (2023).
The second pattern shows a convergence of the values from the i) CIUC test with correction to account for anisotropic consolidation (Su/σ’v0); ii) Nkt from Mayne & Peuchen (2018); and iii) NΔu from Mayne et al. (2023). Also, it can be noted that the FVST shows similar results with these methods below the depth of 6m.
The remolded undrained shear strength is also presented in Figure 6, based on the sleeve friction measurement of the cone (fs) which shows a tendency to decrease over depth, reaching almost zero below 4 m of depth. Figure 6 also shows the results of the remolded undrained shear strength measured by the FVST, which indicates higher values. This difference is probably associated with the inaccuracy of the sleeve load cell used to measure the sleeve friction of the cone penetration, a common issue related to soft soils as already reported by Lunne et al. (1997), McConnell & Wassenaar (2022) and Buò et al. (2022).
Figure 6: Undrained shear strength profile (yield and remolded) of the Bauxite Tailings
Figure 6 shows the yield and the remolded undrained shear strength from the FVST as well the sensitivity (St = Su yield / Su remolded) calculated based on Equation 15, over depth. The results indicate that the sensitivity of the bauxite tailings ranges from 1 to 3 (1 ≤ St ≤ 3), which is classified as a low to medium sensitivity, according to Skempton & Northey (1952). This behavior is in accordance with the observed behavior in the triaxial compression test (CIUC) since no significant strength loss is noted at large strains (ductile behavior).
Conclusion
This paper presents a case study focusing on the evaluation of the undrained shear strength of a bauxite tailing using laboratory and field tests. Also, geotechnical characterization was conducted by laboratory tests (grain-size distribution, Atterberg Limits, and specific gravity). The soil behavior-type classification system proposed by Jefferies & Davies (1991) was used along with the equation proposed by Dos Santos Junior (2021) to represent the boundary suggested by Shuttle & Cunning (2008) to distinguish contractive and dilative behavior. The behavior-based classification shows that the tailings evaluated is a predominantly contractive clay-like geomaterial, which is consistent with the physical classification and the stress-strain behavior shown in the triaxial compression test.
The calculation of the undrained shear strength was performed in the regions where undrained penetration was observed. The criteria used to characterize undrained penetration was based on the pore pressure ratio, as suggested by Schnaid (2009) and the IQ-Bq index suggested by Mayne et al. (2023). Both criteria proved useful to distinguish drained and undrained penetration, but the IQ-Bq index, presented by Mayne et al. (2023) seems to better capture the behavior of the soil, since it incorporates pore pressure (Bq) and the resistance of the soil (Qt).
The comparison of different methodologies using field and laboratory tests to calculate the undrained shear strength of a bauxite tailings was performed. The results have shown that the undrained shear strength determined based on Nkt (Mayne & Peuchen, 2018) and NΔu (Mayne et al., 2023), presented similar values with the CIUC test with the k0 correction to account for anisotropic consolidation and the FVST. The methodology based on the Nke (Mayne et al., 2023) and on NΔu (Mantaras et al., 2014) yielded the Su profile higher than the other bearing capacity factors, in agreement with the profile from the CIUC test without stress correction. This difference highlights the uncertainty in the determination of the undrained shear strength due to the usually unknown horizontal stress. In the tailings examined herein, the authors believe that the lower profile (based on the anisotropic correction of the CIUC), would be the most appropriate, since it agrees well with the FVST and the most often used bearing capacity factors (Nkt and NΔu).
Regarding the remolded undrained shear strength calculated based on the sleeve friction, the results indicated lower values when compared to those measured by the FVST, which highlights the inaccuracy of the sleeve friction measured in very soft soils, as pointed out by McConnell & Wassenaar (2022) and Buò et al. (2022). To deal with this issue, the international standard 22476-1 (ISO, 2022) recommends using friction load cell with accuracy of 5 kPa or 10% when dealing with very soft soils, to obtain reliable results.
The results of the undrained shear strength show the importance of comparing different methodologies based on the CPTu test and with direct measurement of undrained shear strength, such as using CIUC test and the FVST, to define the best methodology to evaluate the stability condition of a TSF. Finally, it is important to highlight that the conclusions obtained in this paper are specific to the bauxite tailings evaluated and the authors do not recommend a direct replication of the results presented herein.
Acknowledgments
The authors would like to acknowledge the support received by Pimenta de Ávila during the develop of this paper.
References
Agaiby, S.S. & Mayne, P.W. 2018. Evaluating undrained rigidity index of clays from piezocone data. Proceedings of the 4th International Symposium on Cone Penetration Testing (CPT’18).
American Society for Testing and Materials – ASTM. 2020. D792-20: Standard Test Methods for Density and Specific Gravity (Relative Density) of Plastics by Displacement.
American Society for Testing and Materials – ASTM. 2008. D2573: Standard Test Method for Field Vane Shear Test in Cohesive Soil.
American Society for Testing and Materials – ASTM. 2007. D422-63: Standard Test Method for Particle-Size Analysis of Soils.
American Society for Testing and Materials – ASTM. 2018. D4318-17e1: Standard Test Methods for Liquid Limit, Plastic Limit, and Plasticity Index of Soils.
Dos Santos Junior, Mauro. 2021. Avaliação da susceptibilidade à liquefação de um rejeito silto-arenoso com base em ensaio CPTu. Dissertação. Universidade Federal de Ouro Preto – UFOP. Núcleo de Geotecnia.
International Organization for Standardization – ISO 22476-1. 2022: Geotechnical investigation and testing — Field testing — Part 1: Electrical cone and piezocone penetration test.
Jefferies, M.G. and Davies, M.P. 1991. Soil classification by the cone penetration test: Discussion. Canadian Geotechnical Journal, 28(1), 173–468
Lunne, T.; Robertson, P.K. & Powell, J.J.M. 1997. Cone Penetration Testing in Geotechnical Practice. First Edition. Abingdon: E & FNSpon Press.
McConnell, A. J. & Wassenaar, J.C. 2022. An innovative new 3MPa CPT – to detect and measure very small fs values. Cone Penetration Testing 2022 (CPT 2022). ISBN 978-1-032-31259-0
B. Di Buò, M. D’Ignazio, T. Länsivaara & M. Haikola. 2022. Issues related to piezocone sleeve friction measurement accuracy in soft sensitive clays. Cone Penetration Testing 2022 (CPT 2022). ISBN 978-1-032-31259-0
Mayne P. W., Ethan, C., James, G. 2023. A CPT Design Parameter Manual.
Mayne, P.W. & Peuchen, J. 2018. Evaluation of CPTU Nkt cone factor for undrained strength of clays. In Proceedings of the 4th International Symposium on Cone Penetration Testing (CPT’18).
Olson, S. M., & Mattson, B. B. 2008. Mode of shear effects on yield and liquefied strength ratios. Canadian geotechnical journal, 45(4), 574-587.
Robertson, P. K., Campanella, R. G., Gillespie, D., & Greig, J. 1986. Use of piezometer cone data. In Use of in situ tests in geotechnical engineering (pp. 1263-1280). ASCE.
Robertson, Peter K. 2010. Estimating in-situ soil permeability from CPT & CPTu. 2nd International Symposium on Cone Penetration Testing, California State Polytechnic University Pomona, CA.
Shuttle, Dawn & Cunning, John. (2007). Liquefaction potential of silts from CPTu. Canadian Geotechnical Journal. Skempton, A. W., and Northey, R. D. 1952. The Sensitivity of Clays, Géotechnique, 3 (1), pp. 30-53.