Guilherme Henrique da Silva Pinto1*, Mauro Pio dos Santos Junior2
1. Pimenta de Ávila Consultoria, Minas Gerais – Brazil, Geotechnical Engineer, guilherme.henrique@pimentadeavila.com.br, +55 31 99680-2136
2. Pimenta de Ávila Consultoria, Minas Gerais – Brazil, Geotechnical Coordinator, mauro.junior@pimentadeavila.com.br, +55 31 99982-5789
ABSTRACT
A correct determination of the tailings’ shear strength is highly important in geotechnical engineering to evaluate the stability condition of a Tailings Storage Facilities (TSF). Commonly, the determination of the undrained shear strength will greatly rely on field investigations, such as the Cone Penetration Test (CPTu), using the classical expression Su = qnet/Nkt, and the Field Vane Test (FVT). In this paper, three methodologies (empirical and/or analytical) were used to estimate the bearing capacity factors (Nkt) based on the CPTu data: i) Vesic (1977) apud Mayne (2016), ii) Mayne & Peuchen (2018) and iii) Robertson (2012) apud Robertson & Cabal (2022). The results highlight that even though the methodologies used in this paper to determine the cone bearing factor (Nkt) were obtained from very different approaches, the profile of the undrained shear strength for the bauxite tailings was reasonably similar with the equation proposed by Mayne & Peuchen (2018) showing values slightly lower than the others. The bauxite tailings’ behavior and the drainage condition were characterized based on de the CPTu data based on Robertson (2016) and Schnaid (2008) methodologies respectively. Also, laboratory assessment was performed.
*Corresponding author: Pimenta de Ávila Consultoria, Geotechnical Engineer, Alameda Oscar Niemeyer, 420 – Vale do Sereno, Nova Lima, Minas Gerais – Brazil, CEP: 34000-000. Phone: +55 31 99680-2136. Email: guilherme.henrique@pimentadeavila.com.br
INTRODUCTION
A correct determination of the tailings’ shear strength is highly important in geotechnical engineering to evaluate the stability condition of a Tailings Storage Facilities (TSF). If the geotechnical parameters related to strength and stiffness are not adequately determined in the early stages of the project, the resulting TSF may either be over-dimensioned or, in the worst situation, it may not present the necessary resilience to withstand the expected loads it will face throughout its life cycle. The importance of the physical and chemical characterization of the tailings is also highlighted in the Global Industry Standard on Tailings Management – GISTM (GISTM, 2020).
To characterize the tailings’ geotechnical behavior and evaluate its shear strength it is important to perform field and laboratory tests. Among the field assessments commercially available, the Field Vane Test (FVT) and Cone Penetration Test (CPTu) are the ones most often used.
The undrained shear strength (Su) can be defined as the soil/tailing’s shear resistance in a saturated or nearly saturated condition, which is mobilized under a fast loading without allowing time for volumetric change (Lunne et al., 1997). In contractile materials, the generated porewater pressures are positive, which reduces the effective stress and, therefore its shear strength. The undrained shear strength (Su) can be calculated by the CPTu using equations based on the bearing capacity factors (Nkt), as described by Equation 6.
This study aims to evaluate different methodologies based on CPTu to determine the undrained shear strength of a bauxite tailings and compare the results with the field vane test (FVT). The behavior of the tailings under shear is evaluated using the Soil Behavior Type Classification System (SBTn) proposed by Robertson (2016). Also, the drainage conditions are evaluated based on Schnaid (2008) propose. Also, laboratory tests were also carried out to evaluate the grain-size distribution curve of the tailings and its Atterberg Limits.
METHODOLOGY
The bauxite tailings characterization was performed using laboratory tests such as those necessary to determine its grain-size distribution (ASTM, D422-63), Atterberg Limits (ASTM, D4318) and moisture content (ASTM, D2216-19). To evaluate the tailings in-situ behavior a CPTu with dissipation tests was performed. Different methodologies based on Nkt were applied to determine the undrained shear strength. The results were compared to the field vane test (FVT) measurements.
Cone Penetration Test (CPTu) Interpretation
The Cone Penetration Test with Pore pressure measurement (CPTu) consists of a 60° cone penetrometer pushing equipment and an automated data acquisition system (ASTM D5778-20 and ISO 22476-1). The standard cone has a cross-sectional area of 10 cm2 or 15 cm2 and a 150 cm2 friction sleeve located above the cone and the penetration is usually carried out at a rate of 2.0 ± 0.5 cm/s, with readings being recorded every 1 cm, 2 cm to 5 cm. CPTu usually provides three main parameters: (i) the cone tip resistance (qc), which characterizes the soil resistance to cone penetration, (ii) the sleeve friction (fs), which represents the soil adhesion to the friction sleeve and (iii) the penetration porewater pressure (u), commonly measured behind the cone tip (u2 location).
In addition to the CPTu penetration process, it is also common to perform porewater pressure dissipation tests, to obtain the in-situ equilibrium porewater pressure profile (u0). The dissipation test consists of a full stop in the cone penetration, followed by the measurement of the porewater pressure over time. Using the u0 relative to its depth, it is possible to estimate the porewater pressure profile, allowing an accurate estimation of the effective stress, which governs the soil’s strength and stiffness.
The cone tip resistance (qc) needs to be corrected to account for the unequal end area effect, which leads to the calculation of the corrected cone resistance (qt). As described by Lunne et al., (1997), the qt value can be calculated as qt = qc + u2(1 − a), where “a” is cone area ratio. In this paper, it was used an “a” value equal to 0.78 as provided by the cone calibration certificate.
To perform the bauxite tailing classification, the Soil Behavior Type Classification System proposed by Robertson (2016) was applied. The author proposed a soil classification system based on the behavior characteristics instead of physical characteristics such as the grain size and plasticity. This classification is based on the normalized cone resistance (Qtn) and the normalized friction ratio (Fr) as detailed in Equations 1 and 2. The stress exponent (n) obtained is approximately equal to 1 to clayey soils (Robertson & Cabal, 2022).
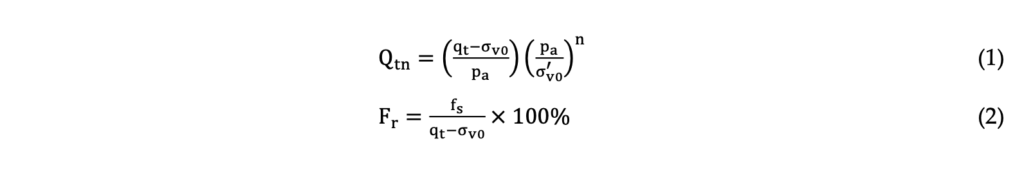
Based on the normalized parameters Robertson (2016) proposed the IB index to divide the soils in three class: i) clay-like behavior, when IB < 22; ii) transitional behavior when 22 < IB < 32; and iii) sand- like behavior, when IB > 32. Also, the author introduces the parameter CD to evaluate if the soil is contractive or dilative under shear. CD values higher than 70 indicates a dilative behavior whereas CD values below 70 indicates a contractive behavior. These parameters can be calculated by Equations 3 and 4.
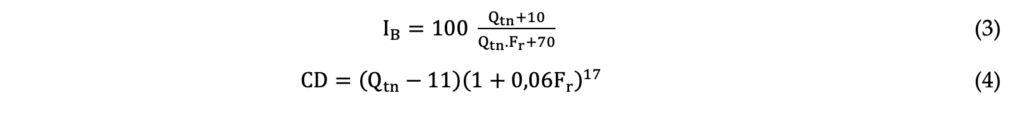
To calculate the undrained shear strength of the bauxite tailing and avoid the regions of partial saturation or partial drainage, it was used the criteria of pore pressure ratio (Bq) higher than 0.30, as suggested by Schnaid (2008). The pore pressure ratio can be calculated using Equation 5.

Undrained Shear Strength Assessment
The undrained shear strength can be calculated from the CPTu using a bearing cone factor (Nkt) according to Equation 6, as indicated by Lunne et al. (1997). To estimate the Nkt, different approaches have been evaluated in this paper, such as the equations proposed by Vesic (1977) apud Mayne (2016), Robertson (2012), apud Robertson & Cabal (2022) and Mayne & Peuchen (2018).
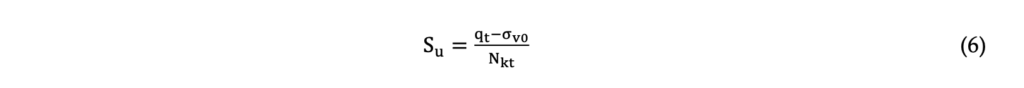
Vesic (1977) apud Mayne (2016)
As detailed by Mayne (2016), the spherical cavity expansion solutions formulated by Vesic (1972, 1977) can be used to predict the undrained shear strength, according to Equation 7 by using the rigidity index (IR). Agaiby & Mayne (2018) used a hybrid formulation of spherical cavity expansion and critical state soil mechanics (SCE-CSSM) to derive a simple solution to calculate the rigidity index (IR) of clays based on CPTu, as indicated by Equation 8. In this equation, the parameter aq is the slope of the u2-σv0 versus qt-σv0 plot and M is the slope of the critical state line in the p’ – q space.
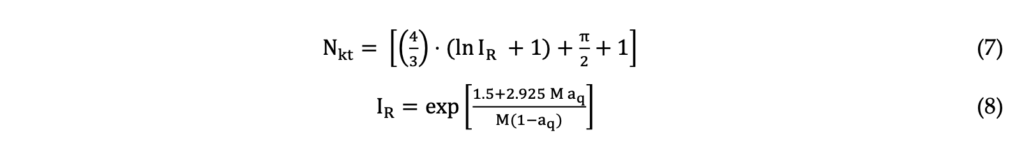
Mayne & Peuchen (2018)
Based on an extensive database of 70 different clay deposits, Mayne & Peuchen (2022) showed the reasonableness and the reliability of the equation proposed earlier by Mayne & Peuchen (2018). As shown by the authors, Nkt varies from values as high as 25 for stiff and overconsolidated clays to values as low as 6 for soft and sensitive clays. In this paper, the Equation 9 proposed by Mayne & Peuchen (2018) will be used to estimate Nkt profile of the bauxite tailings.
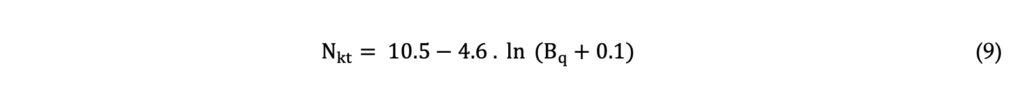
Robertson (2012) apud Robertson & Cabal (2022)
Robertson & Cabal (2022) suggests the use of the Equation 10 proposed by Robertson (2012) to assess the Nkt value based on the normalized friction ratio (Fr).
Nkt = 10.5+7logFr (10)
Field Vane Shear Test
Field Vane Test (FVT) consists of a rotation of a set of cruciform rectangular blades pushed to pre- defined depths. As described by the international standard ASTM D2573M-18 the test can be performed with the blade driven directly into the ground (test type A) or with previous drilling (test type B). The blade’s rotation rate must be controlled, requiring 6.0 ± 0.6 °/min to mobilize an undrained behavior in the tested clay. The undrained shear strength (Su) can be obtained by Equation 11, where T is the torque measured by the equipment (kN.m) and D is the vane diameter (0,063m).
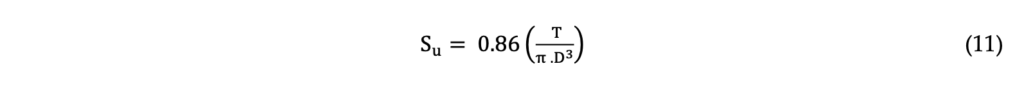
RESULTS AND DISCUSSION
Figure 2 shows the results of the laboratory tests performed to determine the grain-size distribution and the Atterberg Limits. The bauxite tailing presents 40% of clay-size particles, 50% of silt-size particles and 10% of sand. Also, its present a low plasticity as detailed in the plasticity chart.
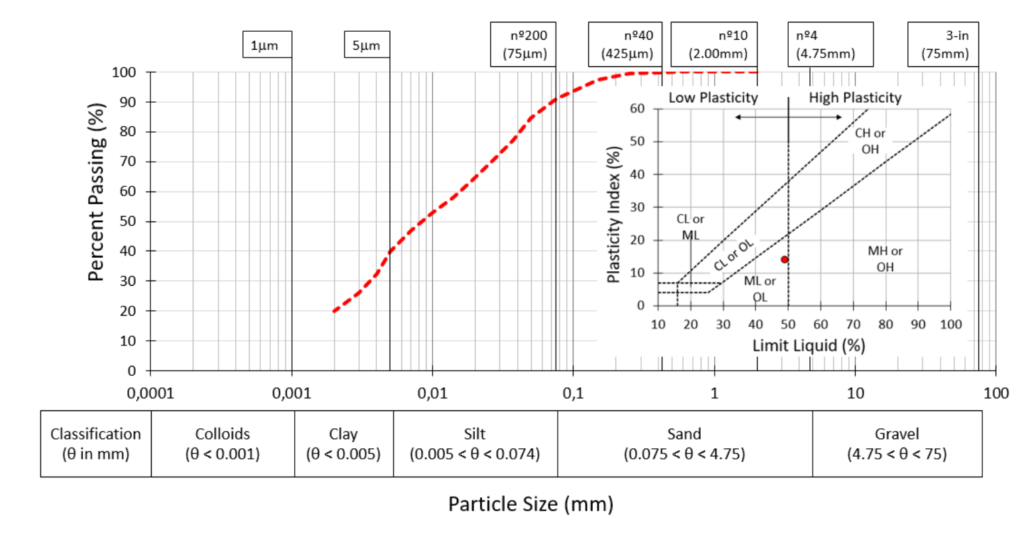
Figure 2 Laboratory tests: grain-size distribution and plasticity chart
Figure 3 shows the data of the CPTu test. The in-situ equilibrium porewater pressure was estimated by an interpolation of the dissipation tests which led to an almost 100% hydrostatic condition. This result and the linear increase of the cone resistance (qt) indicates a normally consolidated behavior as described by Mayne (2016). Also, the moisture content was determined over depth, reaching a mean value of around 60%.
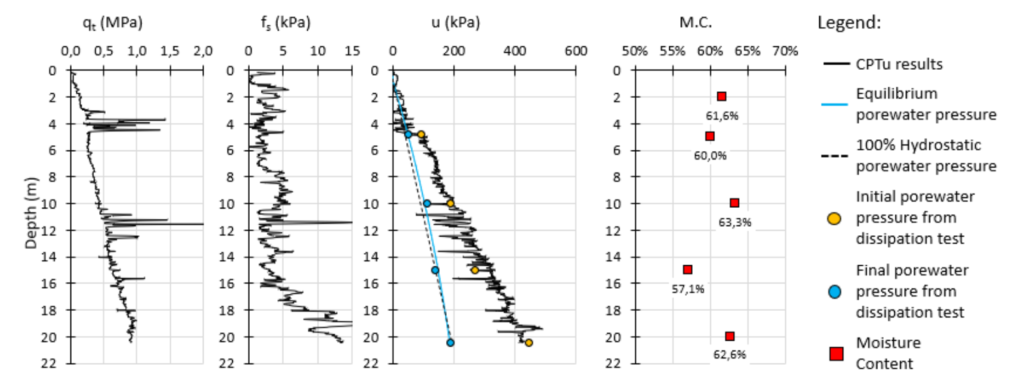
Figure 3 CPTu results and moisture content of the bauxite tailings
The normalized parameters (Qtn, Fr and Bq) of the CPTu performed on the bauxite tailings is shown in Figure 4a. The Bq value is almost 0 near the surface where the tailings are partially saturated due to the dewatering and drying process. At depth below 5m the pore pressure ratio reaches values higher than 0.30 indicating an undrained penetration. Also, using the Soil Behavior Type Classification System proposed by Robertson (2016) it can be shown that the tailings is deposited in a contractive state and shows a clay-like behavior. Figure 4b indicates that higher scatter is observed above 5m correspondent to the region of lower Bq values (less than 0.30). By using the criteria of Bq ≥ 0.30 the scatter of the data is reduced, and the undrained shear strength is calculated for the regions where fully undrained penetration occurred.
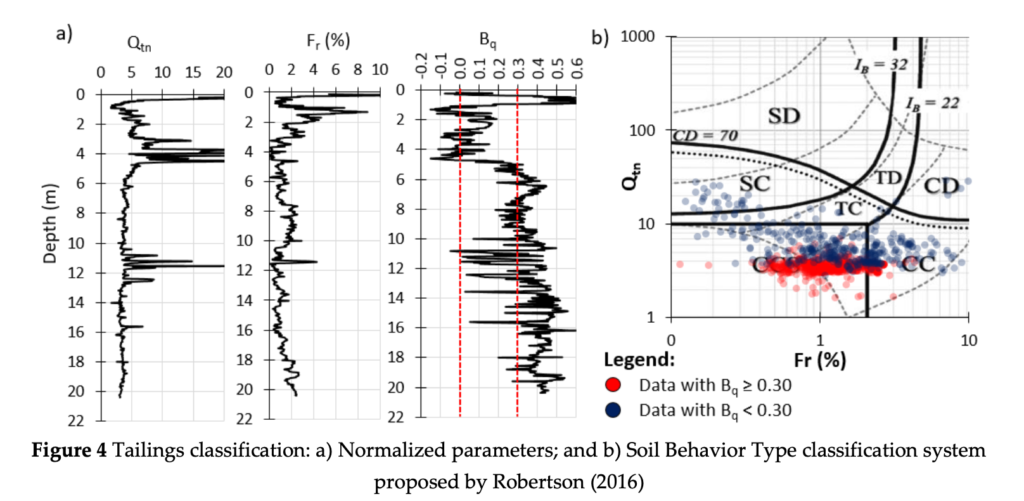
The rigidity index was calculated using the formulation proposed by Agaiby & Mayne (2018). By NTH methodology (Senneset et al., 1989), the mean friction angle obtained is 28o and the corresponding M value is equal to 1.11. As can be seen in Figure 5, the accuracy of the linear relationship between u2-σv0 and qt-σv0 is increased as the data is restricted to values of higher Bq. However, adopting Bq higher than 0.40 would restrict the CPTu data to only 33%. By using the criteria of Bq > 0.30 it was obtained a rigidity index of 196 and Nkt equal to 10.9.

The undrained shear strength profile was calculated using the Equation 6 with cone bearing factors (Nkt) derived from Equations 7 to 10. The results obtained from the CPTu evaluation, along with the undrained shear strength measured from the field vane test (FVT) are shown in Figure 6. The first FVT performed at depth 2m is assumed to be in a partially saturated region, as can be observed by the low values of penetration pore pressure (u2) in Figure 3. The surface of the tailings is exposed to different weather conditions which causes it to reduce its void ratio as it shrinks. Therefore, the undrained shear strength determined by the FVT was higher compared to all methodologies based on the CPTu. This measurement can be disregarded, as it is affected by partial drainage and is not representative of an undrained condition.
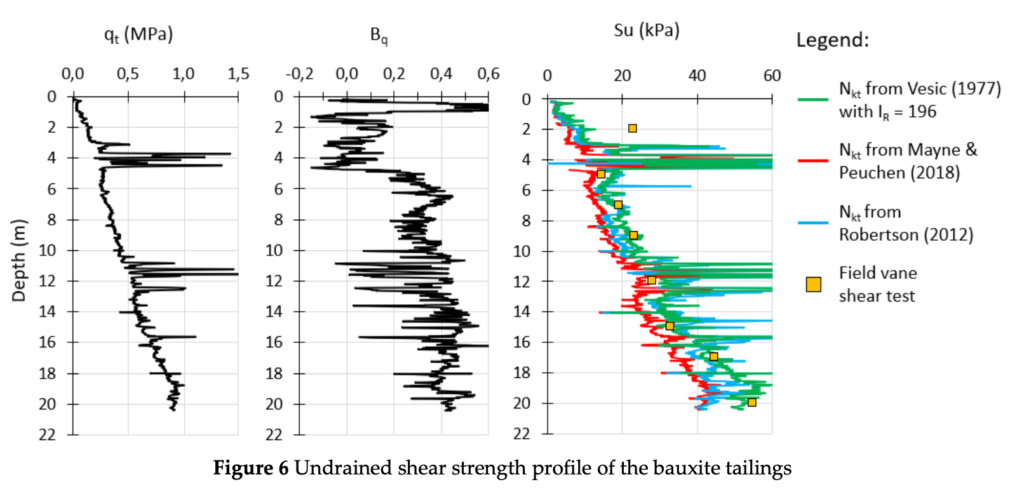
Analyzing the results obtained from the CPTu using the methodologies presented above (Equations 7 to 10), it is possible to note that the Mayne & Peuchen (2018) equation yielded lower values of undrained shear strength as compared to the field vane test (FVT) results. The other methods used in this study (Robertson (2012) and Vesic (1977)) were able to adjust to the FVT results more accurately. Such difference is possibly associated with the mode of shear used to obtain the cone bearing factor (Nkt). The data used by Mayne & Peuchen (2018) to calibrate the Nkt correlation is mainly based on triaxial compression shear mode (CAUC). As shown by Mayne (2016), using the profile of undrained shear strength of the Bothkennar soft clay, the values of undrained shear strength from the FVT mode of shear are higher than those obtained by the triaxial compression shear mode.
The results show that different methodologies, derived from different approaches, varying from a more empirical analysis (such as the Mayne & Peuchen 2018, that uses a database approach) yielded similar values of undrained shear strength from other methods based on more analytical approaches, such as the equations proposed by Vesic (1977) apud Mayne (2016) using the rigidity index (IR) from the hybrid formulation of spherical cavity expansion and based on critical state soil mechanics (SCE- CSSM) proposed by Agaiby & Mayne (2018).
CONCLUSION
The bauxite tailings studied herein was classified as a contractive clay-like soil using the Soil Behavior Type Classification System (SBTn) proposed by Robertson (2016). The laboratory tests show a grain- size distribution composed of 40% of clay-size particles, 50% of silt-size particles and 10% of sand with low plasticity (LL < 50%). The bauxite tailings were classified with a group name of silt and a group symbol ML using the Unified Soil Classification System (ASTM D2487-17).
The calculation of the undrained shear strength was restricted to the regions of high porepressure ration (Bq > 0.30) as suggested by Schnaid (2008), to avoid the region of partially saturated tailings in the surface.
The evaluation of the undrained shear strength was performed in this paper using field tests, such as the CPTu and FVT. Three methods were used to estimate the bearing capacity factors (Nkt) in this paper: i) Vesic (1977) apud Mayne (2016), ii) Mayne & Peuchen (2022) and iii) Robertson (2012) apud Robertson & Cabal (2022). The results indicate that the equation proposed by Mayne & Peuchen (2018) yielded lower values of undrained shear strength as compared to the other methods and the FVT performed. The authors associate such results with the fact that the empirical correlation developed by Mayne & Peuchen (2018), using a database approach, was mainly based on triaxial compression mode of shear which is shown to be lower than the FVT mode of shear as indicated by Mayne (2016) using the profile of undrained shear strength of the Bothkennar soft clay.
Aside from this difference, it is of interest to note that even though the methodologies used in this paper to determine the cone bearing factor (Nkt) were obtained from very different approaches, varying from an empirical correlation (the database approach from Mayne & Peuchen 2018) to a more analytical approach (the equations proposed by Vesic 1977 apud Mayne (2016) using the IR from Agaiby & Mayne 2018) the profile of the undrained shear strength for the bauxite tailings was reasonably similar.
The methodologies used in this paper to assess the Nkt factor have been extensively validated to natural soils. Since tailings are manufactured materials with certain unique characteristics (geochemistry, angularity, etc.) the applicability of these correlations was evaluated for the specific site conditions. The results have shown accuracy of the methodologies employed, depending on the shear mode.
ACKNOWLEDGEMENTS
The author thanks Pimenta de Ávila Consultoria for all the support in the development of this study.
NOMENCLATURE
Su undrained shear strength
Nkt cone bearing factor for net tip resistance
qc cone resistance
qt total cone resistance (corrected)
fs sleeve friction
u porewater pressure generated during cone penetration
u2 porewater pressure generated during cone penetration measured behind the cone u0 equilibrium porewater pressure
σv0 total vertical stress
Fr normalized friction ratio
Qtn normalized cone penetration resistance
Bq pore pressure ratio
n stress exponent
IB Modified Soil Behavior Type index
CD contractive/dilative boundary
IR Rigidity Index
M slope of the critical state line in p’ – q space aq Slope of u2-σv0 (y axis) and qt-σv0 (x axis)
REFERENCES
Agaiby, S. S., & Mayne, P. W. (2018). Evaluating undrained rigidity index of clays from piezocone data. In Cone Penetration Testing 2018 (pp. 65-71). CRC Press.
American Society for Testing and Materials – ASTM (2020). D2487-17: Standard Practice for Classification of Soils for Engineering Purposes (Unified Soil Classification System).
American Society for Testing and Materials – ASTM (2015). D2573: Standard Test Method for Field Vane Shear Test in Cohesive Soil.
American Society for Testing and Materials – ASTM (2007). D422-63: Standard Test Method for Particle-Size Analysis of Soils.
American Society for Testing and Materials – ASTM (2020) D5778: Standard Test Method for Electronic Friction Cone and Piezocone Penetration Testing of Soils.
American Society for Testing and Materials – ASTM (2018) D4318-17e1: Standard Test Methods for Liquid Limit, Plastic Limit, and Plasticity Index of Soils.
American Society for Testing and Materials – ASTM (2019) D2216-19: Standard Test Methods for Laboratory Determination of Water (Moisture) Content of Soil and Rock by Mass.
Global Industry Standard on Tailings Management – GISTM (2020), Global Tailings Review, International Council on Mining & Metals (ICMM), UN Environment Programme (UNEP) and Principles for Responsible Investment (PRI).
International Organization for Standardization – ISO 22476-1 (2022): Geotechnical investigation and testing — Field testing — Part 1: Electrical cone and piezocone penetration test.
Lunne, T.; Robertson, P.K. & Powell, J.J.M. (1997) Cone Penetration Testing in Geotechnical Practice. 1o Edition. Abingdon: E & FNSpon Press.
Mayne, P.W. (2016). Evaluating effective stress parameters and undrained shear strength of soft-firm clays from CPT and DMT. Australian Geomechanics Journal 51 (4): 27-55.
Mayne, P. W., & Peuchen, J. (2018). Evaluation of CPTU Nkt cone factor for undrained strength of clays. In Cone Penetration Testing 2018 (pp. 423-429). CRC Press.
Mayne, P. W., & Peuchen, J. (2022). Undrained shear strength of clays from piezocone tests: A database approach. In Cone Penetration Testing 2022 (pp. 546-551). CRC Press.
Robertson, P. K. (2016). Cone penetration test (CPT)-based soil behavior type (SBT) classification system—an update. Canadian Geotechnical Journal, 53(12), 1910-1927.
Robertson, P.K. & Kelly O Cabal (2022) Guide to Cone Penetration Testing. 7o Edition. Gregg Drilling LLC.
Schnaid, F. (2008). In situ testing in geomechanics: the main tests. CRC Press.
Senneset, K., Sandven, R., & Janbu, N. (1989). Evaluation of soil parameters from piezocone tests. Transportation research record.

